)袋中装有大小相同的黑球、白球和红球共10个。已知从袋中任意摸出1个球,得到黑球的概率是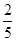 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是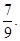
(1)求袋中各色球的个数;
(2)从袋中任意摸出3个球,记得到白球的个数为ξ,求随机变量ξ的分布列及数学期望Eξ和方差Dξ;
推荐套卷
)袋中装有大小相同的黑球、白球和红球共10个。已知从袋中任意摸出1个球,得到黑球的概率是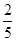 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是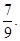
(1)求袋中各色球的个数;
(2)从袋中任意摸出3个球,记得到白球的个数为ξ,求随机变量ξ的分布列及数学期望Eξ和方差Dξ;