如图，抛物线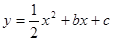
与x轴的两个交点A、B，与y轴交于点C，A点坐标为（4，0），C点坐标（0，－4）．
（1）求抛物线的解析式；
（2）用直尺和圆规作出△ＡＢＣ的外接圆⊙M，（不写作法，保留作图痕迹），并求⊙M的圆心M的坐标；
相关试题
是关于x的一元一次方程，再解这个方程时，粗心的小成误把-x看成x，他解得的解是x=4，你知道原方程的正确解释什么吗？请写出解答过程．
相关知识点
推荐套卷
如图，抛物线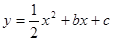与x轴的两个交点A、B，与y轴交于点C，A点坐标为（4，0），C点坐标（0，－4）．
（1）求抛物线的解析式；
（2）用直尺和圆规作出△ＡＢＣ的外接圆⊙M，（不写作法，保留作图痕迹），并求⊙M的圆心M的坐标；
粤公网安备 44130202000953号