如图,已知抛物线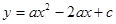 与y轴交于点C,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且
与y轴交于点C,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且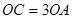 .点E为线段BC上的动点(点E不与点B,C重合),以E为顶点作
.点E为线段BC上的动点(点E不与点B,C重合),以E为顶点作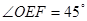 ,射线ET交线段OB于点F.
,射线ET交线段OB于点F.
(1) 求出此抛物线函数表达式,并直接写出直线BC的解析式;
(2)求证: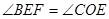 ;
;
(3)当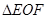 为等腰三角形时,求此时点E的坐标;
为等腰三角形时,求此时点E的坐标;
(4)点P为抛物线的对称轴与直线BC的交点,点M在x轴上,点N在抛物线上,是否存在以点A、M、N、P为顶点的平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
相关知识点
推荐套卷
 有实根.
有实根.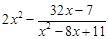 的值.
的值. 与x轴交于A,B两点,与直线
与x轴交于A,B两点,与直线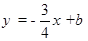 相交于B,C两点,连结A,C两点。
相交于B,C两点,连结A,C两点。
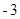 时,有最大值
时,有最大值 ,且当x=0时,y=
,且当x=0时,y= 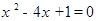 (2)、(x+3)(x-6)=
(2)、(x+3)(x-6)=
 粤公网安备 44130202000953号
粤公网安备 44130202000953号