为丰富高三学生的课余生活，提升班级的凝聚力，某校高三年级6个班（含甲、乙）举行唱歌比赛．比赛通过随机抽签方式决定出场顺序．
求：（1）甲、乙两班恰好在前两位出场的概率；
（2）比赛中甲、乙两班之间的班级数记为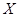
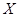，求的分布列和数学期望．
相关试题
，计算
的值
，且
为第三象限角，求
及
的值。
的不等式
．
时，求此不等式的解集；
，求实数
的取值范围．已知函数
，
.
(1)设函数
，求函数
的单调区间；
(2)是否存在实数
，使得方程
在区间
内有且只有两个不相等的实数根？若存在，请求出
的取值范围；若不存在，请说明理由．
：
的右焦点
，过原点和
轴不重合的直线与椭圆
，
两点，且
，
最小值为
．
的切线
与椭圆
，
两点，当
与
是否垂直？若垂直，请给出证明；若不垂直，请说明理由．推荐套卷
为丰富高三学生的课余生活，提升班级的凝聚力，某校高三年级6个班（含甲、乙）举行唱歌比赛．比赛通过随机抽签方式决定出场顺序．
求：（1）甲、乙两班恰好在前两位出场的概率；
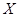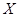（2）比赛中甲、乙两班之间的班级数记为，求的分布列和数学期望．
已知函数，.
(1)设函数，求函数的单调区间；
(2)是否存在实数，使得方程在区间内有且只有两个不相等的实数根？若存在，请求出的取值范围；若不存在，请说明理由．
粤公网安备 44130202000953号