定义:对于各项均为整数的数列 ,如果
,如果 (
( =1,2,3, )为完全平方数,则称数列
=1,2,3, )为完全平方数,则称数列 具有“
具有“ 性质”;不论数列
性质”;不论数列 是否具有“
是否具有“ 性质”,如果存在数列
性质”,如果存在数列 与
与 不是同一数列,且
不是同一数列,且 满足下面两个条件:
满足下面两个条件:
(1) 是
是 的一个排列;
的一个排列;
(2)数列 具有“
具有“ 性质”,则称数列
性质”,则称数列 具有“变换
具有“变换 性质”.
性质”.
给出下面三个数列:
①数列 的前
的前 项和
项和 ;
;
②数列 :1,2,3,4,5;
:1,2,3,4,5;
③数列 :1,2,3,4,5,6,7,8,9,10,11.
:1,2,3,4,5,6,7,8,9,10,11.
具有“ 性质”的为 ;具有“变换
性质”的为 ;具有“变换 性质”的为 .
性质”的为 .
推荐套卷
 和
和 互相垂直,则
互相垂直,则 = .
= . 与直线
与直线 的距离等于 .
的距离等于 . 关于
关于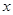 轴的对称点的坐标是________.
轴的对称点的坐标是________.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号