如图,在平面直角坐标系中,点A,B的坐标分别为A(-1,0)、B(3,0)现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C、D,连接AC,BD.
(1)直接写出点C、D的坐标,求四边形ABDC的面积 ;
;
(2)在坐标轴上是否存在一点P,使 =
=
 ,若存在这样一点,求出点P的坐标,若不存在,试说明理由.
,若存在这样一点,求出点P的坐标,若不存在,试说明理由. 

(3)如图,在线段CO上取一点G,使OG=3CG,在线段OB上取一点F,使OF=2BF,CF 与BG交于点H,求四边形OGHF的面积 .
.
相关知识点
推荐套卷
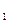 x+b与反比例函数y=
x+b与反比例函数y=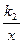 的图象交于A(1,6),B(a,3)两点 .
的图象交于A(1,6),B(a,3)两点 .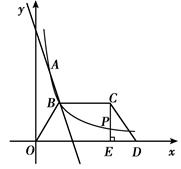
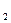 的值;
的值;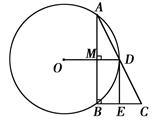
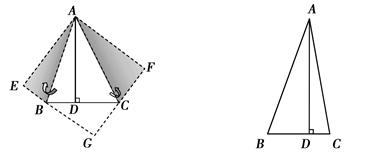
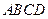 中,过点A分别作AE⊥BC于点E,AF⊥CD于点F.
中,过点A分别作AE⊥BC于点E,AF⊥CD于点F.
 ∠BAE=∠DAF;
∠BAE=∠DAF;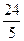 ,
,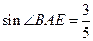 ,求CF的长.
,求CF的长. 粤公网安备 44130202000953号
粤公网安备 44130202000953号