学校为了解全校1600名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.将调查得到的结果绘制成如图所示的频数分布直方图和扇形统计图(均不完整).

(1)在这次调查中,一共抽取了 名学生;
(2)选择“步行”上学的学生有 人;
(3)扇形统计图中,“私家车”所对应扇形的圆心角的度数为 ;
(4)估计全校所有学生中有多少人乘坐公交车上学.
相关知识点
推荐套卷
 千米)
千米) 吨,总运费为
吨,总运费为 元,试写出
元,试写出 ,其中
,其中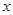 是不等式组
是不等式组 的整数解.
的整数解.
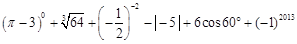 .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号