如图,已知A,B两点的坐标分别为A(0,2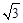 ),B(2,0)直线AB与反比例函数
),B(2,0)直线AB与反比例函数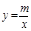 的图像交与点C和点D(-1,
的图像交与点C和点D(-1,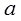 ).
).
(1)求直线AB和反比例函数的解析式;
(2)求∠ACO的度数;
(3)将△OBC绕点O逆时针方向旋转α角(α为锐角),得到△OB′C′,当α为多少度时OC′⊥AB,并求此时线段AB′的长.
推荐套卷
如图,已知A,B两点的坐标分别为A(0,2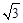 ),B(2,0)直线AB与反比例函数
),B(2,0)直线AB与反比例函数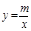 的图像交与点C和点D(-1,
的图像交与点C和点D(-1,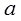 ).
).
(1)求直线AB和反比例函数的解析式;
(2)求∠ACO的度数;
(3)将△OBC绕点O逆时针方向旋转α角(α为锐角),得到△OB′C′,当α为多少度时OC′⊥AB,并求此时线段AB′的长.