如图,Rt△ABC中,BC=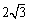 ,∠ACB=90°,∠A=30°,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连结BE1交CD1于D2;过D2作D2E2⊥AC于E2,连结BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点E4、E5、…、E2013,分别记△BCE1、△BCE2、△BCE3、···、△BCE2013的面积为S1、S2、S3、…、S2013.则S2013的大小为( ).
,∠ACB=90°,∠A=30°,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连结BE1交CD1于D2;过D2作D2E2⊥AC于E2,连结BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点E4、E5、…、E2013,分别记△BCE1、△BCE2、△BCE3、···、△BCE2013的面积为S1、S2、S3、…、S2013.则S2013的大小为( ).
A.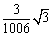 |
B.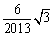 |
C.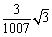 |
D.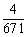 |
相关知识点
推荐套卷
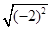 =﹣2
=﹣2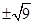 =3
=3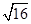 =8
=8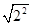 =2
=2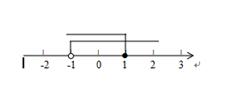
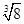
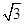
 粤公网安备 44130202000953号
粤公网安备 44130202000953号