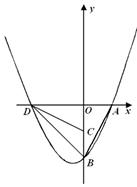
如图,在平面直角坐标系中0A=2,0B=4,将△OAB绕点O顺时针旋转90°至△OCD,若已知抛物线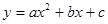 过点A、D、B.
过点A、D、B.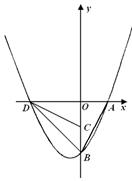
(1)求此抛物线的解析式;
(2)连结DB,将△COD沿射线DB平移,速度为每秒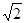 个单位.
个单位.
①经过多少秒O点平移后的O′点落在线段AB上?
②设DO的中点为M,在平移的过程中,点M、A、B能否构成等腰三角形?若能,求出构成等腰三角形时M点的坐标;若不能,请说明理由.
相关知识点
推荐套卷
如图,在平面直角坐标系中0A=2,0B=4,将△OAB绕点O顺时针旋转90°至△OCD,若已知抛物线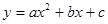 过点A、D、B.
过点A、D、B.

(1)求此抛物线的解析式;
(2)连结DB,将△COD沿射线DB平移,速度为每秒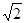 个单位.
个单位.
①经过多少秒O点平移后的O′点落在线段AB上?
②设DO的中点为M,在平移的过程中,点M、A、B能否构成等腰三角形?若能,求出构成等腰三角形时M点的坐标;若不能,请说明理由.