义洁中学计划从荣威公司买A、B两种型号的小黑板,经洽谈,购买一块A型小黑板比购买一块B型小黑板多用20元,且购买5块A型小黑板和4块B型小黑板共需820元。
(1)求购买一块A型小黑板、一块B型小黑板各需要多少元?
(2)根据义洁中学实际情况,需从荣威公司购买A、B两种型号的小黑板共60块,要求购买A、B两种型号小黑板的总费用不超过5240元,并且购买A型小黑板的数量应大于购买A、B两种型号小黑板总数量的 。请你通过计算,求出义洁中学从荣威公司购买A、B两种型号的小黑板有哪几种方案。
。请你通过计算,求出义洁中学从荣威公司购买A、B两种型号的小黑板有哪几种方案。
相关知识点
推荐套卷
 已知矩形广场地面的长为100米,宽为80米.图案设计如图所示:广场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,阴影部分铺绿色地面砖,其余部分铺白色地面砖.
已知矩形广场地面的长为100米,宽为80米.图案设计如图所示:广场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,阴影部分铺绿色地面砖,其余部分铺白色地面砖.
 中,
中,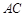 与
与 相交于点
相交于点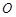 ,AB⊥AC,CD⊥BD.
,AB⊥AC,CD⊥BD.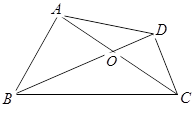
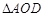 ∽
∽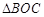 ;
; ,
,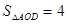 ,求
,求 的值
的值 交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.
交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.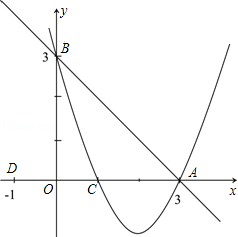
 粤公网安备 44130202000953号
粤公网安备 44130202000953号