如图，点P是菱形ABCD的对角线BD上一点，
连结CP并延长，交AD于E，交BA的延长线于点F．试问：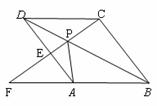
(1)图中△APD与哪个三角形全等？并说明理由．
(2)猜想：线段PC、PE、PF之间存在什么关系？并说明理由．
＋︱－3︱．
-1)¸
，其中a＝
．
．若结果等于
，求出相应a的值．
中，
，
，过点
作
∥
，点
、
分别是射线
上的动点，且
，过点
∥
交线段
于点
，联接
，设
面积为
，
．
的代数式表示
；
，若
与
的长．
； (2)
．相关知识点
推荐套卷
如图，点P是菱形ABCD的对角线BD上一点，
连结CP并延长，交AD于E，交BA的延长线于点F．试问：
(1)图中△APD与哪个三角形全等？并说明理由．
(2)猜想：线段PC、PE、PF之间存在什么关系？并说明理由．
粤公网安备 44130202000953号