已知抛物线 (
(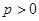 )上一点
)上一点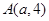 到其准线的距离为
到其准线的距离为 .
.
(Ⅰ)求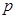 与
与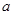 的值;
的值;
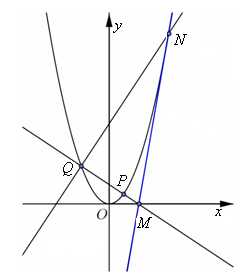
(Ⅱ)设抛物线 上动点
上动点 的横坐标为
的横坐标为 (
(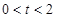 ),过点
),过点 的直线交
的直线交 于另一点
于另一点 ,交
,交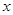 轴于
轴于 点(直线
点(直线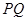 的斜率记作
的斜率记作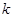 ).过点
).过点 作
作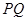 的垂线交
的垂线交 于另一点
于另一点 .若
.若 恰好是
恰好是 的切线,问
的切线,问 是否为定值?若是,求出该定值;若不是,说明理由.
是否为定值?若是,求出该定值;若不是,说明理由.
相关知识点
推荐套卷
已知抛物线 (
(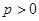 )上一点
)上一点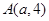 到其准线的距离为
到其准线的距离为 .
.
(Ⅰ)求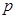 与
与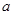 的值;
的值;
(Ⅱ)设抛物线 上动点
上动点 的横坐标为
的横坐标为 (
(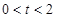 ),过点
),过点 的直线交
的直线交 于另一点
于另一点 ,交
,交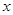 轴于
轴于 点(直线
点(直线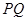 的斜率记作
的斜率记作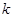 ).过点
).过点 作
作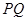 的垂线交
的垂线交 于另一点
于另一点 .若
.若 恰好是
恰好是 的切线,问
的切线,问 是否为定值?若是,求出该定值;若不是,说明理由.
是否为定值?若是,求出该定值;若不是,说明理由.