如图,四边形ABCD中, 为正三角形,
为正三角形,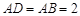 ,
,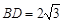 ,AC与BD交于O点.将
,AC与BD交于O点.将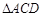 沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为
沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为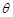 ,且P点在平面ABCD内的射影落在
,且P点在平面ABCD内的射影落在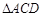 内.
内.
(Ⅰ)求证: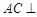 平面PBD;
平面PBD;
(Ⅱ)若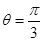 时,求二面角
时,求二面角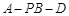 的余弦值。
的余弦值。
推荐套卷
如图,四边形ABCD中, 为正三角形,
为正三角形,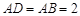 ,
,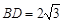 ,AC与BD交于O点.将
,AC与BD交于O点.将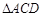 沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为
沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为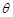 ,且P点在平面ABCD内的射影落在
,且P点在平面ABCD内的射影落在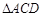 内.
内.
(Ⅰ)求证: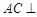 平面PBD;
平面PBD;
(Ⅱ)若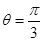 时,求二面角
时,求二面角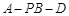 的余弦值。
的余弦值。