已知椭圆具有性质:若 是椭圆
是椭圆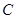 :
: 且
且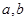 为常数
为常数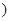 上关于原点对称的两点,点
上关于原点对称的两点,点 是椭圆上的任意一点,若直线
是椭圆上的任意一点,若直线 和
和 的斜率都存在,并分别记为
的斜率都存在,并分别记为 ,
, ,那么
,那么 与
与 之积是与点
之积是与点 位置无关的定值
位置无关的定值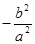 .
.
试对双曲线 且
且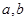 为常数
为常数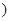 写出类似的性质,并加以证明.
写出类似的性质,并加以证明.
推荐套卷
已知椭圆具有性质:若 是椭圆
是椭圆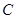 :
: 且
且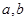 为常数
为常数 上关于原点对称的两点,点
上关于原点对称的两点,点 是椭圆上的任意一点,若直线
是椭圆上的任意一点,若直线 和
和 的斜率都存在,并分别记为
的斜率都存在,并分别记为 ,
, ,那么
,那么 与
与 之积是与点
之积是与点 位置无关的定值
位置无关的定值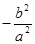 .
.
试对双曲线 且
且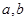 为常数
为常数 写出类似的性质,并加以证明.
写出类似的性质,并加以证明.