已知函数f(x) ="lnx" g(x) =-
(1)当a=1时,若曲线y=f(x)在点M (x0,f(x0))处的切线与曲线y=g(x)在点P (x0, g(x0))处的切线平行,求实数x0的值;
(II)若 (0,e],都有f(x)≥g(x)
(0,e],都有f(x)≥g(x) 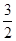 ,求实数a的取值范围.
,求实数a的取值范围.
推荐套卷
已知函数f(x) ="lnx" g(x) =-
(1)当a=1时,若曲线y=f(x)在点M (x0,f(x0))处的切线与曲线y=g(x)在点P (x0, g(x0))处的切线平行,求实数x0的值;
(II)若 (0,e],都有f(x)≥g(x)
(0,e],都有f(x)≥g(x) 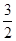 ,求实数a的取值范围.
,求实数a的取值范围.