如图1,在直角梯形 中,AD//BC,
中,AD//BC, 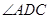 =900,BA="BC" 把ΔBAC沿
=900,BA="BC" 把ΔBAC沿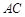 折起到
折起到 的位置,使得点
的位置,使得点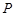 在平面ADC上的正投影O恰好落在线段
在平面ADC上的正投影O恰好落在线段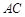 上,如图2所示,点
上,如图2所示,点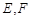 分别为线段PC,CD的中点.
分别为线段PC,CD的中点.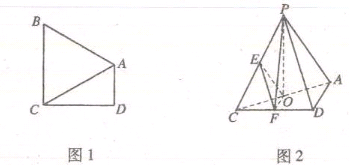
(I) 求证:平面OEF//平面APD;
(II)求直线CD 与平面POF
与平面POF
(III)在棱PC上是否存在一点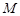 ,使得
,使得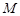 到点P,O,C,F四点的距离相等?请说明理由.
到点P,O,C,F四点的距离相等?请说明理由.
推荐套卷
如图1,在直角梯形 中,AD//BC,
中,AD//BC, 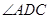 =900,BA="BC" 把ΔBAC沿
=900,BA="BC" 把ΔBAC沿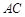 折起到
折起到 的位置,使得点
的位置,使得点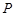 在平面ADC上的正投影O恰好落在线段
在平面ADC上的正投影O恰好落在线段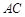 上,如图2所示,点
上,如图2所示,点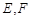 分别为线段PC,CD的中点.
分别为线段PC,CD的中点.
(I) 求证:平面OEF//平面APD;
(II)求直线CD 与平面POF
与平面POF
(III)在棱PC上是否存在一点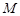 ,使得
,使得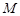 到点P,O,C,F四点的距离相等?请说明理由.
到点P,O,C,F四点的距离相等?请说明理由.