已知a＝2(
，)，b＝(，
)(其中0＜
＜1)，函数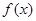
＝a·b，若直线
＝
是函数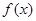图象的一条对称轴．
(Ⅰ)试求的值；
(Ⅱ)若函数y＝
的图象是由y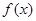＝的图象的各点的横坐标伸长到原来的2倍，然后再向左平移
个单位长度得到，求y＝的单调递增区间．
,
,
,设
. 
的最小正周期. (Ⅱ)若
,且
,求
的值.
，
，求
的值．
的值；（II）若
且
，求
的值。
，其中
，记函数
的图像中两条相邻对称轴间的距离
，求
及
，求最大值。
中，
，
．（Ⅰ）求
的值；（Ⅱ）设
，求推荐套卷
已知a＝2(，)，b＝(，)(其中0＜＜1)，函数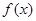＝a·b，若直线＝是函数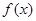图象的一条对称轴．
(Ⅰ)试求的值；
(Ⅱ)若函数y＝的图象是由y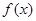＝的图象的各点的横坐标伸长到原来的2倍，然后再向左平移个单位长度得到，求y＝的单调递增区间．
粤公网安备 44130202000953号