已知椭圆C：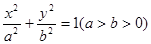
的两个焦点为F1、F2，点P在椭圆C上，且|PF1|=
,
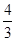|PF2|=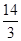
， PF1⊥F1F2.
（1）求椭圆C的方程；(6分)
（2）若直线L过圆x2+y2+4x-2y=0的圆心M交椭圆于A、B两点，且A、B关于点M对称，求直线L的方程.
相关试题
的最小值为
.
求
及此时
的最大值.(12分)
图象的一条对称轴是直线
.
的值；
上的图像.(12分)
的值；
的值.(12分)
在R上是偶函数.
的值；
在
上是增函数.(12分)
.
的最小正周期；
时，求
的集合.(12分)推荐套卷
已知椭圆C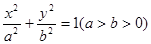：的两个焦点为F1、F2，点P在椭圆C上，且|PF1|=,
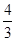|PF2|=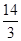 ， PF1⊥F1F2.
（1）求椭圆C的方程；(6分)
（2）若直线L过圆x2+y2+4x-2y=0的圆心M交椭圆于A、B两点，且A、B关于点M对称，求直线L的方程.
粤公网安备 44130202000953号