【问题】如图,在正方形ABCD内有一点P,PA=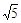 ,PB=
,PB=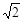 ,PC=1,求∠BPC的度数.
,PC=1,求∠BPC的度数.
分析根据已知条件比较分散的特点,我们可以通过旋转变换将分散的已知条件集中在一起,于是将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图),然后连结PP′.
解决问题请你通过计算求出图17-2中∠BPC的度数;
【类比研究】如图,若在正六边形ABCDEF内有一点P,且PA=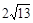 ,PB=4,PC=2.
,PB=4,PC=2.
(1)∠BPC的度数为 ;(2)直接写出正六边形ABCDEF的边长为 .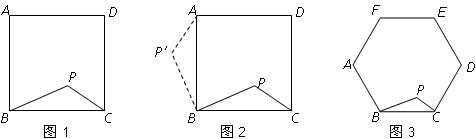
相关知识点
推荐套卷
 ,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC.
,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC. 
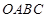 的顶点
的顶点 分别在
分别在 轴和
轴和 轴上,点
轴上,点 的坐标为
的坐标为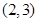 .双曲线
.双曲线 的图像经过
的图像经过 的中点
的中点 ,且与
,且与 交于点
交于点 ,连接
,连接 .
.
 的值及点
的值及点 是边上一点,且ΔFCB∽ΔDBE,求直线
是边上一点,且ΔFCB∽ΔDBE,求直线 的解析式
的解析式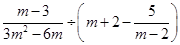 ,其中
,其中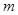 是方程
是方程 的根.
的根.
 ,四边形AEPF的面积为
,四边形AEPF的面积为 ,求
,求 粤公网安备 44130202000953号
粤公网安备 44130202000953号