阅读下面材料:解答问题
为解方程 (x2-1)2-5 (x2-1)+4=0,我们可以将(x2-1)看作一个整体,然后设 x2-1=y,那么原方程可化为 y2-5y+4=0,解得y1=1,y2=4.
当y=1时,x2-1=1,∴x2=2,∴x=±;当y=4时,x2-1=4,∴x2=5 ,∴x=±,
,∴x=±,
故原方程的解为 x1=,x2=-,x3=,x4=-.
上述解题方法叫 做换元法;
做换元法;
请利用换元法解方程.(x 2-x)2 - 4 (x 2-x)-12=0
相关知识点
推荐套卷
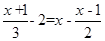
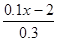 +
+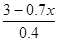 =1.
=1. 粤公网安备 44130202000953号
粤公网安备 44130202000953号