某海边旅游景点有50辆自行车供游客租赁使用,管理这些自行车的费用是每日115元。根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超出6元,则每超过1元,租不出的自行车就增加3辆。为了便于结算,每辆自行车的日租金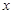 (元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用
(元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用 (元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得).
(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得).
(Ⅰ)求函数 的解析式及其定义域;
的解析式及其定义域;
(Ⅱ)试问当每辆自行车的日租金定为多少元时,才能使一日的净收入最多?
推荐套卷
 :
: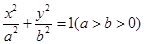 的离心率
的离心率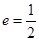 ,右焦点到直线
,右焦点到直线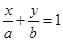 的距离
的距离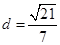 ,
, 为坐标原点
为坐标原点 与椭圆
与椭圆 两点,以
两点,以 为直径的圆过原点
为直径的圆过原点
 名学生被考官D面试,求
名学生被考官D面试,求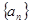 的公差大于0,且
的公差大于0,且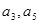 是方程
是方程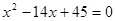 的两根,数列
的两根,数列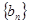 的前n项的和为
的前n项的和为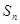 ,且
,且 .
.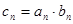 ,求证:
,求证: .
.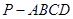 中,
中,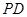
 底面
底面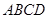 ,且底面
,且底面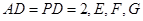 分别为
分别为 的中点.
的中点.
 平面
平面 ;
; 和平面
和平面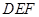 的夹角.
的夹角. .
. 的最小正周期和单调递增区间;
的最小正周期和单调递增区间; 时,
时,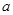 的值,并求出
的值,并求出 的对称轴方程.
的对称轴方程. 粤公网安备 44130202000953号
粤公网安备 44130202000953号