如图,在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C坐标为(-1,0),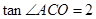 .一次函数
.一次函数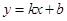 的图象经过点B、C,反比例函数
的图象经过点B、C,反比例函数 的图象经过点B.
的图象经过点B.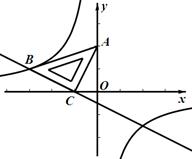
(1)求一次函数和反比例函数的关系式;
(2)直接写出当x<0时, 的解集;
的解集;
(3)在 轴上找一点M,使得AM+BM的值最小,并求出点M的坐标和AM+BM的最小值.
轴上找一点M,使得AM+BM的值最小,并求出点M的坐标和AM+BM的最小值.
推荐套卷
如图,在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C坐标为(-1,0),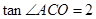 .一次函数
.一次函数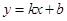 的图象经过点B、C,反比例函数
的图象经过点B、C,反比例函数 的图象经过点B.
的图象经过点B.
(1)求一次函数和反比例函数的关系式;
(2)直接写出当x<0时, 的解集;
的解集;
(3)在 轴上找一点M,使得AM+BM的值最小,并求出点M的坐标和AM+BM的最小值.
轴上找一点M,使得AM+BM的值最小,并求出点M的坐标和AM+BM的最小值.