设函数f(x)=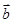
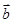×，其中向量
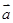="(2cosx,1)," 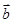=(cosx,
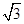sin2x+m)．
(1)求函数f(x)的最小正周期和f(x)在[0, p]上的单调递增区间；
(2)当xÎ[0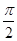
]时,ô f(x)ô <4恒成立，求实数m的取值范围．
，
，
，
，且
，求实数
的取值范围．
的不等式：
；②
．
．
．
，且
，
，
，则
．
．
中至少有一个不小于0．
则
是
的什么条件？
，且
，推荐套卷
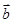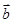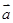设函数f(x)= ×，其中向量="(2cosx,1)," 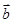=(cosx, 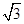sin2x+m)．
(1)求函数f(x)的最小正周期和f(x)在[0, p]上的单调递增区间；
(2)当xÎ[0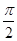]时,ô f(x)ô <4恒成立，求实数m的取值范围．
粤公网安备 44130202000953号