小刚很擅长球类运动,课外活动时,足球队、篮球队都力邀他到自己的阵营,小刚左右为难,最后决定通过掷硬币来确定。游戏规则如下:连续抛掷硬币三次,如果三次正面朝上或三次反面朝上,则由小刚任意挑选两球队;如果两次正面朝上一次正面朝下,则小刚加入足球阵营;如果两次反面朝上一次反面朝下,则小刚加入篮球阵营。
(1)用画树状图的方法表示三次抛掷硬币的所有结果。
(2)小刚任意挑选两球队的概率有多大?
(3)这个游戏规则对两个球队是否公平?为什么?
相关知识点
推荐套卷
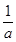 =
=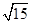 ,求a+
,求a+

 粤公网安备 44130202000953号
粤公网安备 44130202000953号