阅读以下材料,并解决相应问题:
小明在课外学习时遇到这样一个问题:
定义:如果二次函数
,
、
、
是常数)与
,
、
、
是常数)满足
,
,
,则这两个函数互为“旋转函数”.求函数
的旋转函数,小明是这样思考的,由函数
可知,
,
,
,根据
,
,
,求出
,
,
就能确定这个函数的旋转函数.
请思考小明的方法解决下面问题:
(1)写出函数
的旋转函数.
(2)若函数
与
互为旋转函数,求
的值.
(3)已知函数
的图象与
轴交于
、
两点,与
轴交于点
,点
、
、
关于原点的对称点分别是
、
、
,试求证:经过点
、
、
的二次函数与
互为“旋转函数”.
 、
、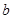 表示小冬从小丽、小兵袋子中抽出的卡片上标有的数字,请用树状图法或列表法写出(
表示小冬从小丽、小兵袋子中抽出的卡片上标有的数字,请用树状图法或列表法写出( ,
,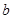 ) 的所有取值;
) 的所有取值; ,
,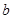 )在一次函数
)在一次函数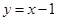 图像上的概率.
图像上的概率.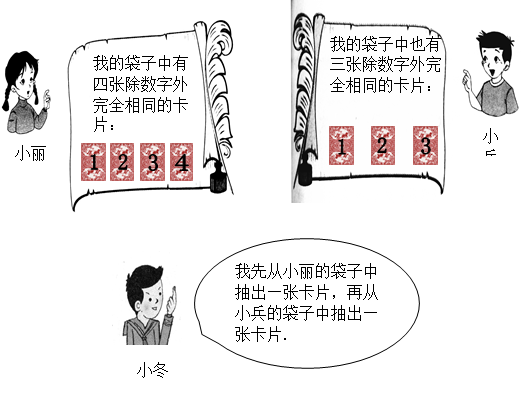
 、
、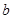 表示小冬从小丽、小兵袋子中抽出的卡片上标有的数字,请用树状图法或列表法写出(
表示小冬从小丽、小兵袋子中抽出的卡片上标有的数字,请用树状图法或列表法写出( ,
,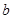 ) 的所有取值;
) 的所有取值; ,
,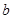 )在一次函数
)在一次函数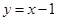 图像上的概率.
图像上的概率.