如图,某城市设立以城中心 为圆心、
为圆心、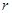 公里为半径的圆形保护区,从保护区边缘起,在城中心
公里为半径的圆形保护区,从保护区边缘起,在城中心 正东方向上有一条高速公路
正东方向上有一条高速公路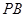 、西南方向上有一条一级公路
、西南方向上有一条一级公路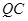 ,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆
,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆 相切的直道
相切的直道 .已知通往一级公路的道路
.已知通往一级公路的道路 每公里造价为
每公里造价为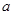 万元,通往高速公路的道路
万元,通往高速公路的道路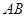 每公里造价是
每公里造价是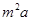 万元,其中
万元,其中 为常数,设
为常数,设 ,总造价为
,总造价为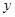 万元.
万元.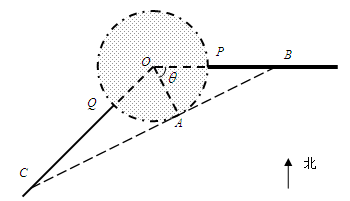
(1)把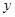 表示成
表示成 的函数
的函数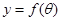 ,并求出定义域;
,并求出定义域;
(2)当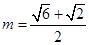 时,如何确定A点的位置才能使得总造价最低?
时,如何确定A点的位置才能使得总造价最低?
相关知识点
推荐套卷
 的前
的前 项和为
项和为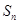 ,且对任意正整数
,且对任意正整数 都在直线
都在直线 上.求数列
上.求数列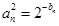 设
设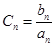 求:数列
求:数列 前
前 .
. 是正数组成的数列,其前
是正数组成的数列,其前 项和为
项和为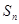 ,且对所有的正整数
,且对所有的正整数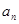 与2的等差中项等于
与2的等差中项等于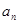
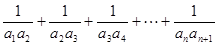
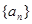 的前n项和为Sn,且满足
的前n项和为Sn,且满足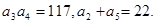
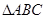 中,A、B、C的对边分别是a、b、c,且A、B、C成等差数列.
中,A、B、C的对边分别是a、b、c,且A、B、C成等差数列.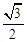 .
. 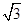 ,求:a,c的值.
,求:a,c的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号