如图所示，已知在圆锥SO中，底面半径r＝1，母线长l＝4，M为母线SA上的一个点，且SM＝x，从点M拉一根绳子，围绕圆锥侧面转到点A，求：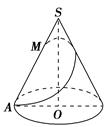
(1)设f(x)为绳子最短长度的平方，求f(x)表达式；
(2)绳子最短时，顶点到绳子的最短距离；
(3)f(x)的最大值．
相关试题
，其图像在点
处的切线为
．
、直线
及两坐标轴围成的图形绕
轴旋转一周所得几何体的体积；
轴围成图形的面积．
．
时，求
的极小值；
对任意的
都不是曲线
的切线，求
的取值范围.
的前n项和为Sn ,且满足
。
；
，并用数学归纳法证明。
的展开式中，第6项为常数项.
的项的系数；
是数列
的前
项和，且
的通项公式；
中，所有满足
的正整数
的个数称为这个数列
（n为正整数），求数列
的前
，若
对
恒成立，求正整数
的最小值。相关知识点
推荐套卷
如图所示，已知在圆锥SO中，底面半径r＝1，母线长l＝4，M为母线SA上的一个点，且SM＝x，从点M拉一根绳子，围绕圆锥侧面转到点A，求：
(1)设f(x)为绳子最短长度的平方，求f(x)表达式；
(2)绳子最短时，顶点到绳子的最短距离；
(3)f(x)的最大值．
粤公网安备 44130202000953号