已知椭圆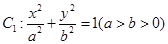 的离心率为
的离心率为 ,
,
 轴被抛物线
轴被抛物线 截得的线段长等于
截得的线段长等于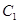 的长半轴长.
的长半轴长.
(1)求 的方程;
的方程;
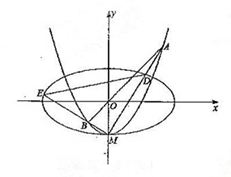
(2)设 与
与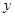 轴的交点为
轴的交点为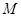 ,过坐标原点
,过坐标原点 的直线
的直线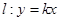
与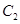 相交于
相交于 两点,直线
两点,直线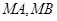 分别与
分别与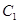 相交于
相交于 .
.
①证明: 为定值;
为定值;
②记 的面积为
的面积为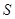 ,试把
,试把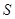 表示成
表示成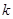 的函数,并求
的函数,并求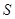 的最大值.
的最大值.
推荐套卷
已知椭圆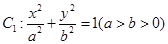 的离心率为
的离心率为 ,
,
 轴被抛物线
轴被抛物线 截得的线段长等于
截得的线段长等于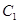 的长半轴长.
的长半轴长.
(1)求 的方程;
的方程;
(2)设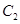 与
与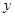 轴的交点为
轴的交点为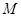 ,过坐标原点
,过坐标原点 的直线
的直线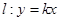
与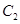 相交于
相交于 两点,直线
两点,直线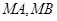 分别与
分别与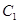 相交于
相交于 .
.
①证明: 为定值;
为定值;
②记 的面积为
的面积为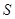 ,试把
,试把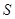 表示成
表示成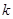 的函数,并求
的函数,并求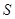 的最大值.
的最大值.