如图,在 中,AB=AC=10cm, BC=16cm,DE=4cm.线段DE(端点D从点B开始)沿BC边以1cm/s的速度向点C运动,当端点E到达点C时停止运动.过点E作EF∥AC交AB于点F,连接DF,设运动的时间为t秒(t≥0).
中,AB=AC=10cm, BC=16cm,DE=4cm.线段DE(端点D从点B开始)沿BC边以1cm/s的速度向点C运动,当端点E到达点C时停止运动.过点E作EF∥AC交AB于点F,连接DF,设运动的时间为t秒(t≥0).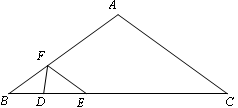
(1)用含t的代数式表示线段EF的长度为 ;
(2)在运动过程中,△DEF能否为等腰三角形?若能,请求出t的值;若不能,试说明理由.
(3)设M、N分别是DF、EF的中点,请直接写出在整个运动过程中,线段MN所扫过的图形的面积.
相关知识点
推荐套卷

 的形状,并说明理由;
的形状,并说明理由;


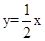 的图像相交于点(2,m).
的图像相交于点(2,m).
 粤公网安备 44130202000953号
粤公网安备 44130202000953号