已知函数 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,有
时,有 (其中
(其中 为自然对数的底,
为自然对数的底, ).
).
(1)求函数 的解析式;
的解析式;
(2)设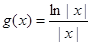 ,
,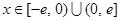 ,求证:当
,求证:当 时,
时, ;
;
(3)试问:是否存在实数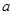 ,使得当
,使得当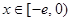 时,
时, 的最小值是3?如果存在,求出实数
的最小值是3?如果存在,求出实数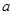 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
相关知识点
推荐套卷
已知函数 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,有
时,有 (其中
(其中 为自然对数的底,
为自然对数的底, ).
).
(1)求函数 的解析式;
的解析式;
(2)设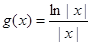 ,
,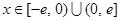 ,求证:当
,求证:当 时,
时, ;
;
(3)试问:是否存在实数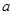 ,使得当
,使得当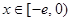 时,
时, 的最小值是3?如果存在,求出实数
的最小值是3?如果存在,求出实数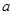 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.