如图,长方形ABCD被分成六个小的正方形,已知中间一个小正方形的边长为2,其它正方形的边长分别为 .观察图形并探索:
.观察图形并探索:
(1)填空: ,
,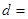 ;(用含
;(用含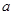 的代数式表示)
的代数式表示)
(2)求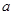 的值.
的值.
相关知识点
推荐套卷
如图,长方形ABCD被分成六个小的正方形,已知中间一个小正方形的边长为2,其它正方形的边长分别为 .观察图形并探索:
.观察图形并探索:
(1)填空: ,
,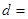 ;(用含
;(用含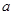 的代数式表示)
的代数式表示)
(2)求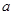 的值.
的值.