已知三棱锥S—ABC的底面是正三角形，A点在侧面SBC上的射影H是△SBC的垂心.
(1)求证：BC⊥SA
(2)若S在底面ABC内的射影为O，证明：O为底面△ABC的中心；
(3)若二面角H—AB—C的平面角等于30°，SA=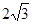
，求三棱锥S—ABC的体积.
是第二象限的角，试分别确定2
,
+
)=-
,且
(n∈Z).
+k
)=-2cos(
;
sin2
cos2
+cos
,
).求值：
.推荐套卷
已知三棱锥S—ABC的底面是正三角形，A点在侧面SBC上的射影H是△SBC的垂心.
(1)求证：BC⊥SA
(2)若S在底面ABC内的射影为O，证明：O为底面△ABC的中心；
(3)若二面角H—AB—C的平面角等于30°，SA=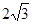，求三棱锥S—ABC的体积.
粤公网安备 44130202000953号