如图1,在Rt△ABC中,∠C=90°,BC=6,AC=3,D,E分别是AC,AB上的点,且DE∥BC,DE=4,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2. 
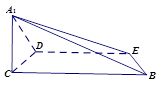
图1 图2
(1)求证:A1C⊥平面BCDE;
(2)过点E作截面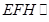
平面
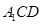,分别交CB于F,
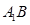于H,求截面
的面积;
(3)线段BC上是否存在点P,使平面A1DP与平面A1BE成
的角?说明理由.
的图象与x轴有两个不同的交点
、
，且
，试问该二次函数的图象由
的图象向上平移几个单位得到？
的定义域．
前
项和为
，若
，求数列的公比
．
是(－
+
+4，求
[1,2]时解析式
，求
的定义域
上为减函数，求
的范围推荐套卷
如图1,在Rt△ABC中,∠C=90°,BC=6,AC=3,D,E分别是AC,AB上的点,且DE∥BC,DE=4,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.
图1 图2
(1)求证:A1C⊥平面BCDE;
(2)过点E作截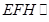面平面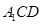,分别交CB于F,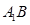于H,求截面的面积;
(3)线段BC上是否存在点P,使平面A1DP与平面A1BE成的角?说明理由.
粤公网安备 44130202000953号