如图,抛物线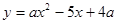 与
与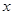 轴相交于点
轴相交于点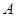 、
、 ,且经过点
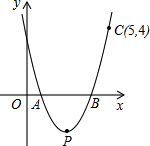
,且经过点 (5,4).该抛物线顶点为
(5,4).该抛物线顶点为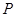 .
.
(1)求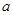 的值和该抛物线顶点
的值和该抛物线顶点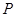 的坐标.
的坐标.
(2)求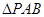 的面积;
的面积;
(3)若将该抛物线先向左平移4个单位,再向上平移2个单位,求出平移后抛物线的解析式.
相关知识点
推荐套卷
如图,抛物线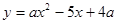 与
与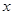 轴相交于点
轴相交于点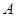 、
、 ,且经过点
,且经过点 (5,4).该抛物线顶点为
(5,4).该抛物线顶点为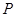 .
.
(1)求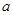 的值和该抛物线顶点
的值和该抛物线顶点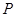 的坐标.
的坐标.
(2)求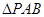 的面积;
的面积;
(3)若将该抛物线先向左平移4个单位,再向上平移2个单位,求出平移后抛物线的解析式.