已知:如图,二次函数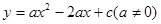 的图象与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
的图象与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
(1)求该二次函数的关系式;
(2)写出该二次函数的对称轴和顶点坐标;
(3)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;
(4)若平行于x轴的动直线 与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线
与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线 ,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由。
,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由。
相关知识点
推荐套卷
 ,且
,且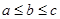 ,若
,若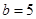 ,求出所有合条件的三角形的另两边
,求出所有合条件的三角形的另两边 ,合条件三角形共多少个?
,合条件三角形共多少个? ,
,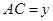 ,
, ,若AB绕B点旋转,CD点旋转,直至A、D两点正好重合于点E为止,形成一个三角形,那么,下面三个不等式中哪些必须成立,并证明你的结论.①
,若AB绕B点旋转,CD点旋转,直至A、D两点正好重合于点E为止,形成一个三角形,那么,下面三个不等式中哪些必须成立,并证明你的结论.① ②
② ③
③

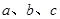 为三角形的三边.求证:
为三角形的三边.求证: .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号