如图，一个被等分成了3个相同扇形的圆形转盘，3个扇形分别标有数字1、
3、6，指针的位置固定，转动转盘后任其自由停止，其中的某个扇形会恰好停止在指针所指的位
置（指针指向两个扇形的交线时，重新转动转盘）.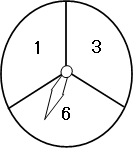
（1）请用画树形图或列表的方法(只选其中一种)，表示出分别转动转盘两次转盘自由停止后，指针所指扇形数字的所有结果；
（2）求分别转动转盘两次转盘自由停止后，指针所指扇形的数字之和的算术平方根为无理数的概率.
相关试题
．
，当
为多少时，图中的两个三角形相似．
在线段
上，
是等边三角形．（1）当
满足怎样的关系式时
；（2）当
的度数．
中，
是
上的一点，
，在
上是否存在一点
，使
三点组成的三角形与
的长；如果不存在，请说明理由．
分别为边
的三等分点（即：
），若
，求
的大小．
相关知识点
推荐套卷
粤公网安备 44130202000953号