设F1、F2分别为椭圆C：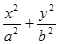
=1（a＞b＞0）的左、右两个焦 点。（1）若椭圆C上的点A（1，
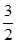）到F1、F2两点的 距离之和等于4，写出椭圆C的方程和焦点坐标；
（2）设点K是（1）中所得椭圆上的动点，求线段F1K的中点的轨迹方程.
相关试题
－4（x－y）（y－z）＝0,求证：x、y、z成等差数列。
，又知顶点C的对边c上的高等于4
,求△ABC的三边a、b、c及三内角。
}的前n项的和为S
＝12，S
>0，S
<0 。
、S
、…、S
－1）对满足|m|≤2的一切实数m的取值都成立。求x的取值范围。
，公差
，求满足
的正整数k；推荐套卷
设F1、F2分别为椭圆C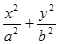： =1（a＞b＞0）的左、右两个焦 点。（1）若椭圆C上的点A（1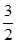，）到F1、F2两点的 距离之和等于4，写出椭圆C的方程和焦点坐标；
（2）设点K是（1）中所得椭圆上的动点，求线段F1K的中点的轨迹方程.
粤公网安备 44130202000953号