已知：点P为正方形ABCD内部一点，且∠BPC=90°，过点P的直线分别交边AB、边CD于点E、点F．
（1）如图1，当PC=PB时，则S△PBE、S△PCF S△BPC之间的数量关系为 _________ ；
（2）如图2，当PC=2PB时，求证：16S△PBE+S△PCF=4S△BPG；
（3）在（2）的条件下，Q为AD边上一点，且∠PQF=90°，连接BD，BD交QF于点N，若S△bpc=80，BE=6．求线段DN的长．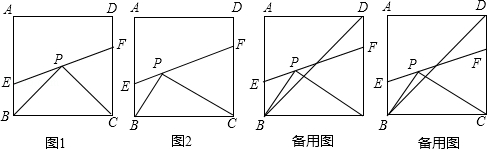
，你能算出∠DAC的度数吗？
图，AD∥BC，∠D＝100°，AC平分∠BCD，求∠DAC的度数．
移，△ABC的边AB移到了EF，作出平移后的三角形（不写作法，保留作图痕迹）．
相关知识点
推荐套卷
已知：点P为正方形ABCD内部一点，且∠BPC=90°，过点P的直线分别交边AB、边CD于点E、点F．
（1）如图1，当PC=PB时，则S△PBE、S△PCF S△BPC之间的数量关系为 _________ ；
（2）如图2，当PC=2PB时，求证：16S△PBE+S△PCF=4S△BPG；
（3）在（2）的条件下，Q为AD边上一点，且∠PQF=90°，连接BD，BD交QF于点N，若S△bpc=80，BE=6．求线段DN的长．
粤公网安备 44130202000953号