如图,在平面直角坐标系中,点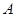 是反比例函数
是反比例函数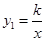
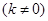 图象上一点,
图象上一点,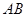 ⊥
⊥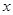 轴于
轴于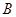 点,一次函数
点,一次函数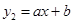
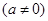 的图象交
的图象交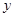 轴于
轴于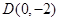 ,交
,交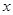 轴于
轴于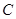 点,并与反比例函数的图象交于
点,并与反比例函数的图象交于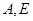 两点,连接
两点,连接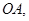 若△
若△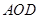 的面积为4,且
的面积为4,且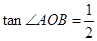 .
.
(1) 分别求出该反比例函数和一次函数的解析式;
(2) 求△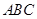 的面积.
的面积.
相关知识点
推荐套卷
如图,在平面直角坐标系中,点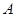 是反比例函数
是反比例函数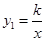
 图象上一点,
图象上一点,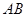 ⊥
⊥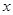 轴于
轴于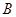 点,一次函数
点,一次函数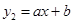
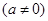 的图象交
的图象交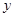 轴于
轴于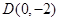 ,交
,交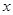 轴于
轴于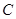 点,并与反比例函数的图象交于
点,并与反比例函数的图象交于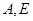 两点,连接
两点,连接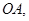 若△
若△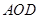 的面积为4,且
的面积为4,且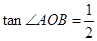 .
.
(1) 分别求出该反比例函数和一次函数的解析式;
(2) 求△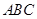 的面积.
的面积.