定义在 上的函数
上的函数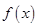 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列 ,
, 仍是等比数列,则称
仍是等比数列,则称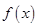 为“保等比数列函数”. 现有定义在
为“保等比数列函数”. 现有定义在 上的如下函数:
上的如下函数:
①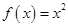 ②
②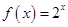 ③
③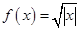 ④
④
则其中是“保等比数列函数”的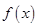 的序号为( )
的序号为( )
| A.①② | B.③④ | C.①③ | D.②④ |
相关知识点
推荐套卷
定义在 上的函数
上的函数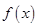 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列 ,
, 仍是等比数列,则称
仍是等比数列,则称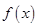 为“保等比数列函数”. 现有定义在
为“保等比数列函数”. 现有定义在 上的如下函数:
上的如下函数:
①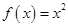 ②
②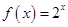 ③
③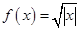 ④
④
则其中是“保等比数列函数”的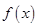 的序号为( )
的序号为( )
| A.①② | B.③④ | C.①③ | D.②④ |