已知A，B两点在抛物线C：x2＝4y上，点M(0,4)满足
＝λ
.
(1)求证：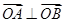
；
(2)设抛物线C过A、B两点的切线交于点N.
(ⅰ)求证：点N在一条定直线上；
(ⅱ)设4≤λ≤9，求直线MN在x轴上截距的取值范围．
相关试题
（
的单位为:秒,
的单位为:米/秒）的速度作变速直线运动,求该物体从时刻
秒至时刻
秒间运动的路程?
,函数
时,求函数
的表达式;
,函数
上的最小值是2 ,求
的值;
与函数
的值以及
的实部的取值范围;
,求证：
为纯虚数.
满足
,
并推测
的表达式;
为斜三棱柱
的侧棱
上一点
交
于点
，
交
于点
.在任意
中有余弦定理：
.拓展到空间，类比三角形的余弦定理，写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式.
推荐套卷
已知A，B两点在抛物线C：x2＝4y上，点M(0,4)满足＝λ.
(1)求证：；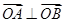
(2)设抛物线C过A、B两点的切线交于点N.
(ⅰ)求证：点N在一条定直线上；
(ⅱ)设4≤λ≤9，求直线MN在x轴上截距的取值范围．
粤公网安备 44130202000953号