某校从高一年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六组: ,
,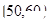 ,…,
,…,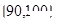 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.
(Ⅰ)求图中实数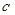 的值;
的值;
(Ⅱ)若该校高一年级共有学生500人,试估计该校高一年级在这次考试中成绩不低于60分的人数;
(Ⅲ)若从样本中数学成绩在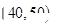 与
与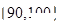 两个分数段内的学生中随机选取两名学生,试用列举
两个分数段内的学生中随机选取两名学生,试用列举
法求这两名学生的数学成绩之差的绝对值不大于10的概率.
相关知识点
推荐套卷
某校从高一年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六组: ,
,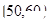 ,…,
,…,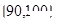 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.
(Ⅰ)求图中实数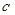 的值;
的值;
(Ⅱ)若该校高一年级共有学生500人,试估计该校高一年级在这次考试中成绩不低于60分的人数;
(Ⅲ)若从样本中数学成绩在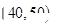 与
与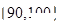 两个分数段内的学生中随机选取两名学生,试用列举
两个分数段内的学生中随机选取两名学生,试用列举
法求这两名学生的数学成绩之差的绝对值不大于10的概率.