如图1，已知双曲线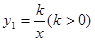
与直线
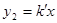交于A,B两点，点A在第一象限.试解答下列问题:
⑴若点A的坐标为（3，1），则点B的坐标为 ；
⑵当x满足： 时，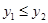
；
⑶过原点O作另一条直线l，交双曲线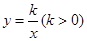
于P,Q两点，点P在第一象限， 如图2所示.
①四边形APBQ一定是 ；
② 若点A的坐标为（3，1），点P的横坐标为1，求四边形APBQ的面积；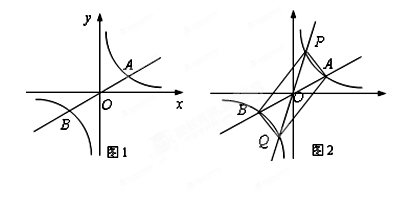
∠CAB．
，求BC和BF的长．
其中
．
，其中
。
，求代数式
的值．相关知识点
推荐套卷
如图1，已知双曲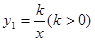线与直线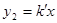交于A,B两点，点A在第一象限.试解答下列问题:
⑴若点A的坐标为（3，1），则点B的坐标为 ；
⑵当x满足： 时，；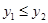
⑶过原点O作另一条直线l，交双曲线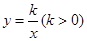于P,Q两点，点P在第一象限， 如图2所示.
①四边形APBQ一定是 ；
② 若点A的坐标为（3，1），点P的横坐标为1，求四边形APBQ的面积；
粤公网安备 44130202000953号