小亮和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍.设两人出发x min后距出发点的距离为y m.图中折线表示小亮在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).
(1)A点所表示的实际意义是 ;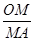 = ;
= ;
(2)求出AB所在直线的函数关系式;
(3)如果小刚上坡平均速度是小亮上坡平均速度
的一半,那么两人出发后多长时间第一次相遇?
相关知识点
推荐套卷
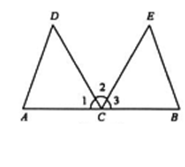
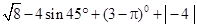
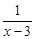 ·
·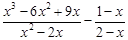 ,然后再取一个你喜爱的
,然后再取一个你喜爱的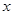 的值代入求值.
的值代入求值. 中,抛物线
中,抛物线 与
与 轴交于点
轴交于点 ,与
,与 轴交于
轴交于 两点,点
两点,点 的坐标为
的坐标为 ,直线
,直线 恰好经过B、C两点.
恰好经过B、C两点.
 的坐标;
的坐标; 在抛物线的对称轴上,抛物线顶点为D且
在抛物线的对称轴上,抛物线顶点为D且 ,求点
,求点 中,AD⊥BC,
中,AD⊥BC,

 外接圆⊙O;
外接圆⊙O;
 粤公网安备 44130202000953号
粤公网安备 44130202000953号