如图，抛物线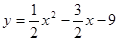
与x轴交于A、B两点，与y轴交于点C，连接BC、AC。
（1）求AB和OC的长；
（2）点E从点A出发，沿x轴向点B运动（点E与点A、B不重合）。过点E作直线l平行BC，交AC于点D。设AE的长为m，△ADE的面积为s，求s关于m的函数关系式，并写出自变量m的取值范围；
（3）在（2）的条件下，连接CE，求△CDE面积的最大值；此时，求出以点E为圆心，与BC相切的圆的面积（结果保留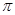
）。
相关试题
为坐标原点
过点
，且圆心
到直线
，若
是圆
满足
，求动点
为正方形
所在平面外一点
平面
分别是线段
的中点。w. （Ｉ）求证：
平面
平面
；
与
所成角的大小。
已知直线
经过点
。
的值；
过点
且
，求直线
正切值；
在直线
上．数列满足： 
，且
，前9项和为153．推荐套卷
如图，抛物线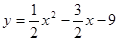与x轴交于A、B两点，与y轴交于点C，连接BC、AC。
（1）求AB和OC的长；
（2）点E从点A出发，沿x轴向点B运动（点E与点A、B不重合）。过点E作直线l平行BC，交AC于点D。设AE的长为m，△ADE的面积为s，求s关于m的函数关系式，并写出自变量m的取值范围；
（3）在（2）的条件下，连接CE，求△CDE面积的最大值；此时，求出以点E为圆心，与BC相切的圆的面积（结果保留）。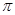
粤公网安备 44130202000953号