已知:线段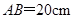 .
.
(1)如图,点 沿线段
沿线段 自
自 点向
点向 点以
点以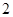 厘米/秒运动,点
厘米/秒运动,点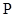 出发
出发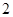 秒后,点
秒后,点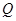 沿线段
沿线段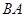 自
自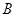 点向
点向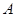 点以
点以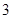 厘米/秒运动,问再经过几秒后
厘米/秒运动,问再经过几秒后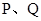 相距
相距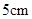 ?
?
(2)如图: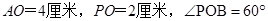 ,点
,点 绕着点
绕着点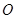 以
以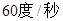 的速度逆时针旋转一周停止,同时点
的速度逆时针旋转一周停止,同时点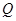 沿直线
沿直线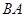 自
自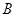 点向
点向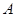 点运动,假若点
点运动,假若点 两点能相遇,求点
两点能相遇,求点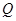 运动的速度 .
运动的速度 . 
相关知识点
推荐套卷
已知:线段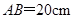 .
.
(1)如图,点 沿线段
沿线段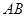 自
自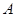 点向
点向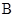 点以
点以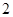 厘米/秒运动,点
厘米/秒运动,点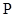 出发
出发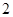 秒后,点
秒后,点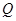 沿线段
沿线段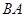 自
自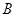 点向
点向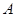 点以
点以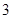 厘米/秒运动,问再经过几秒后
厘米/秒运动,问再经过几秒后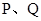 相距
相距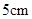 ?
?
(2)如图: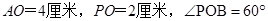 ,点
,点 绕着点
绕着点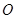 以
以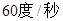 的速度逆时针旋转一周停止,同时点
的速度逆时针旋转一周停止,同时点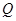 沿直线
沿直线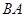 自
自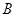 点向
点向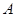 点运动,假若点
点运动,假若点 两点能相遇,求点
两点能相遇,求点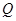 运动的速度 .
运动的速度 . 