（如图，已知∠AOB=ll0°，∠AOC=m∠AOD，∠COE=n∠BOC，且3（m－2）＋4=m＋2，单项式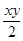
的系数为n．
（1）求4(m-n) 2-(m-n) 2-5的值；
（2）当∠COD：∠COE=3：2时，试求∠COD的度数.
相关试题
，其中
.
－2x－3=0．相关知识点
推荐套卷
（如图，已知∠AOB=ll0°，∠AOC=m∠AOD，∠COE=n∠BOC，且3（m－2）＋4=m＋2，单项式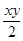的系数为n．
（1）求4(m-n) 2-(m-n) 2-5的值；
（2）当∠COD：∠COE=3：2时，试求∠COD的度数.
粤公网安备 44130202000953号