抛物线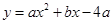 经过
经过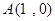 、
、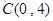 两点,与
两点,与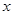 轴交于另一点
轴交于另一点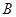 .
.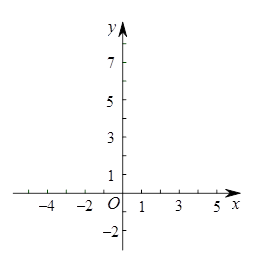
(1)求抛物线的解析式;
(2)已知点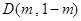 在第二象限的抛物线上,求点
在第二象限的抛物线上,求点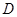 关于直线
关于直线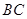 的对称点的坐标;
的对称点的坐标;
(3)在(2)的条件下,连接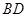 ,点
,点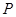 为y轴
为y轴
上一点,且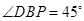 ,求出点
,求出点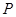 的坐标.
的坐标.
相关知识点
推荐套卷
抛物线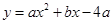 经过
经过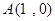 、
、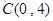 两点,与
两点,与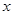 轴交于另一点
轴交于另一点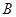 .
.
(1)求抛物线的解析式;
(2)已知点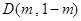 在第二象限的抛物线上,求点
在第二象限的抛物线上,求点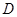 关于直线
关于直线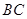 的对称点的坐标;
的对称点的坐标;
(3)在(2)的条件下,连接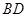 ,点
,点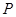 为y轴
为y轴
上一点,且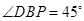 ,求出点
,求出点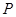 的坐标.
的坐标.