如图，△ABC的高AD=4，BC=8,MNPQ是△ABC中任意一个内接矩形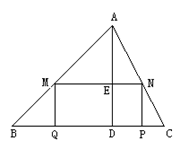
（1）设MN=x，MQ=y,求y关于x的函数解析式；
（2）设MN=x,矩形MNPQ的面积为s，求s与x的函数关系式，并求出当MN为多大时，矩形MNPQ面积s有最大值，最大值为多少？
（3）－
（4）（－5）3
，即
，即
等于什么，并通过计算验证你的猜想。
= 0。相关知识点
推荐套卷
如图，△ABC的高AD=4，BC=8,MNPQ是△ABC中任意一个内接矩形
（1）设MN=x，MQ=y,求y关于x的函数解析式；
（2）设MN=x,矩形MNPQ的面积为s，求s与x的函数关系式，并求出当MN为多大时，矩形MNPQ面积s有最大值，最大值为多少？
粤公网安备 44130202000953号